Rumus Volume Kubus, Volume Kubus, Rumus Kubus, Jaring-Jaring Kubus, Sisi Kubus, Luas Kubus, Luas Permukaan Kubus, Sifat Kubus, Cara Mudah Top Up Saldo Allo Bank Melalui Semua Rekening.
Hello Bestie Quipper Co Id, pada perjumpaan kali ini kembali akan mimin sampaikan pembahasan materi makalah tentang ilmu pelajaran matematika yaitu kubus.
Namun pada perjumpaan sebelumnya, yang mana mimin juga telah menyampaikan materi makalah matematika tentang Fibonacci.
Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini, maka mari bestie simak ulasan mimin selengkapnya di bawah ini.
Daftar Isi :
Pengertian Kubus

Kubus ialah merupakan bentuk bangun ruang tiga dimensi yang di batasi dengan enam bidang kongruen yang berbentuk bujur sangkar atau juga persegi.
Ciri – ciri pada kubus yaitu mempunyai sebanyak 12 rusuk, dan 8 titik sudut, juga 6 sisi. Kalau bestie mau tau penjelasan tentang unsur – unsur kubus, lanjutkan baca artikel ini ya bestie.
Unsur – Unsur Kubus
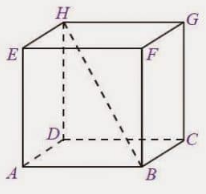
Rusuk
Rusuk merupakan garis yang berpotongan antar dua sisi bidang kubus dan dapat dilihat seperti kerangka yang menyusun bentuk kubus.
Kubus mempunyai 12 rusuk. Perhatikan gambar kubus di atas, yang dimaksud dengan rusuk ialah AB, BC, CD, DA, AE, BF, CG, DH, EF, FG, GH, dan HE.
Titik Sudut
Titik Sudut merupakan titik yang berpotongan antara dua atau 3 rusuk. Kubus mempunyai 8 buah titik sudut.
Perhatikan gambar kubus yang berada di atas, yang merupakan titik pada sudut ialah A, B, C, D, E, F, G, dan H.
Sisi Bidang Kubus
Sisi bidang kubus ialah bidang sisi yang membatasi antar kubuus. Kubus mempunyai 6 sisi yang berbeda.
Perhatikan gambar kubua di atas, yang merupakan sisi bidang kubus pada gambar kubus diatas ialah (ABCD), (EFGH), (ABFE), (DCGH), (BCGF), dan (ADHE).
Diagonal Bidang Sisi
Diagonal Bidang sisi ialah merupakan ruas garis yang saling mengkaitkan antara dua titik sudut yang saling berhadapan pada setiap bidang atau sisi kubus.
Kubus mempunyai 12 diagonal sisi bidang. Perhatikan bidang ABEF pada gambar kubuss ABCD, EFGH di bawah ini :
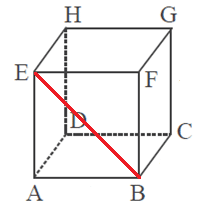
Yang dimaksud dengan diagonal bidang pada kubus ialah : AF, BE, BG, CF, CH, DG, DE, AH, AC, BD, EG, dan HF.
Diagonal bidang pada sisi dapat di tentukan dengan menggunakan teorema phytagoras. Perhatikan gambar kubus di bawah ini :
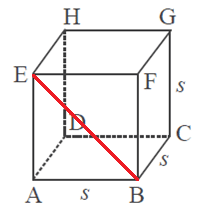
Selanjutnya panjang BE dapat di hitung dengan menggunakan cara teorema phytagoras, yang mana bentuk segitiga ABE siku – siku di A selanjutnya mendapatkan jumlah :
- BE=√(AB2+AE2)
- BE=√(s2+s2)
- BE=√2s2
- BE=s√2
Contohnya diagonal pada bidang kubus ialah B maka secara umum diagonal bidang kubu dapat di rumuskan seperti dibawah ini :
b=s√2
Bidang Diagonal Kubus
Bidang diagonal dalam suatu kubus ialah merupakan bidang yang di batasi oleh dua rusuk dan dua diagonal bidang dalam suatu kubus.
Ada 6 bidang diagonal pada Kubus. Perhatikan contoh gambar di bawah ini :
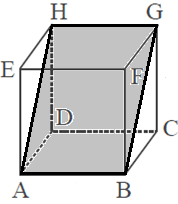
Bidang ABGH sering disebut bidang diagonal, selain itu yang merupakan bidang diagonal ialah ACGE, AFGD, CDEF, BFHD, dan BEHC.
Coba perhatikan kembali gambar kubus ABCD, EFGH di atas, jika diketahui rusuknya s, maka luas bidang ABGH ialah :
- Luas ABGH=ABxBG
- Luas ABGH=sxs√2
- Luas ABGH=s2√2
Sifat – Sifat Kubus
Setelah sebelumnya mimin baru saja menyelesaikan penjelasan tentang unsur – unsur dari kubus, nah sekarang mimin akan menjelaskan tentang sifat – sifat kubus ya bestie. Simak ulasan dibawah ini :
- Semua sisi kubus mempunyai bentuk seperti persegi.
- Semua rusuk kubus mempunyai ukuran sama panjang.
- Dietiap diagonal bidang pada kubus mempunyai ukuran yang memiliki panjang yang sama.
- Setiap diagonal ruang yang dimiliki kubus mempunyai ukuran yang sama panjang.
- Disetiap bidang diagonal pada kubus mempunyai bentuk persegi panjang.
Itulah bestie penjelasan tentang sifat – sifat kubus, selanjutnya dibawah ini mimin akan menjelaskan tentang jaring – jaring kubus, langsung saja lanjutkan membacanya ya bestie.
Jaring – Jaring Kubus
Jaring – Jaring ialah merupakan bidang datar yaitu merupakan gabungan dari bangun datar yang memiliki bentuk seperti bentuk bangun ruang misalnya kubus, balok, limas beserta lainnya.
Jaring – jaring bisa di dapatkan dengan cara membagi bentuk berupa bangun ruang dengan cara mengikuti rusuk – rusuknya.
Di bawah ini mimin akan membahas jaring – jaring pada kubus yang terdiri dari 6 buah bangun datar persegi atau bujur sangkar.
Dibawah ini adalah merupakan contoh gambar jaring – jaring pada kubus :
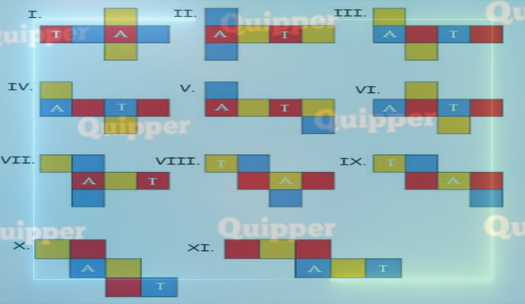
Keterangan :
- A = Alas
- T = Tutup
Rumus Kubus
Mengenai rusmus kubus ini, akan dibagi 7, sebaiknya bestie lihat susunan rumus yang mimin siapkan dibawah ini :
1. Luas Permukaan
L = 6xS2
2. Volume
Volum = S3 atau sxsxs
K =12 x S
3. Diagonal Bidang/sisi
Ds =S√2
4. Diagonal Bidang Seluruhnya
Dss = 12 x S√2
5. Diagonal Ruang
Dr = S√3
Drr : 4. S√3
6. Luas Bidang Diagonal
Bd = S2√2
7. Luas Bidang Diagonal Seluruh
Bd = 6 x S2√2
Contoh Soal Rumus Volume Kubus
Berikut ini ada beberapa contoh soal dari mimin yang membahas pelajaran matematika tentang bidang kubus, coba bestie selesaikan contoh soal dibawah ini :
Contoh Soal 1
Dyna akan mengirimkan paket kepada saudaranya yang berupa 125 souvenir akan di kemas ke dalam kotak berbentuk kubus kecil yang mempunyai panjang 4 cm.
Sebelum dikirim, souvenir tersebut akan dimasukkan kedalam kardus besar yang berbentuk kubus hingga kardus dapat terisi penuh.
Tentukan ukuran panjang kotak kardus besar yang akan digunakan dyna.
Penyelesaian
- Diketahui :
Jumlah souvenir : 125
Rusuk kotak pada souvenir : 4 cm
- Ditanya :
Panjang rusuk kotak besar(s)?
- Jawab :
Volume kubus besar : 125 satuan kubus kecil
S3 = 125
S = 3√125
S = 5 satuan kubu kecil
S kubus besar = 5 satuan kubus x panjang rusuk kubus
S kubus besar = 5 x 4 cm
S kubus besar = 20 cm
Jadi, panjang rusuk pada kotak besar adalah 20 cm.
Contoh Soal 2
Sebuah akuarium yang memiliki bentuk kubus mempunyai volume 512 liter. Berapa cm tinggi akuarium tersebut?
Penyelesaian
- Diketahui :
Volume akuarium = 512 liter atau 512 dm3.
- Ditanya :
Tinggi akuarium atau rusuk (s)?
- Jawab :
Volume = S3
512 = S3
S = 3√512
S = 8 dm
S = 80 cm
Jadi, tinggi akuarium tersebut ialah 80 cm.
Aplikasi Pemecah Soal Matematika
Dijaman sekarang ini tidak heran kalau anak – anak lebih sering bertanya pada google dari pada bertanya pada orang tuanya.
Karena sekarang semua – semuanya bisa dicari digoole. Nah salah satu aplikasi yang baru saja di keluarkan oleh google play store adalah Qanda.
Qanda ini jenis aplikasi yang bisa membantu bestie menjawab soal – soal matematika dengan cepat, cara downloadnya mudah.
Bestie bisa mencarinya di google play store dengan mengetikan Aplikasi Qanda, atau juga bestie bisa langsung klik link ini.
Akhir Kata
Nah demikianlah pembahasan materi makalah kali ini dari mimin tentang kubus. Semoga bermanfaat dan dapat membantu bestie – bestie semua.
Lalu jika bestie ingin mencari pelajaran matematika lainnya, bestie bisa mencarinya di quipper.co.id. Karena mimin banyak menyediakan pelajaran matematika di web tersebut.
Sekian dan Terima Kasih!
