SiSimpangan Rata-Rata Data Tersebut Adalah, 2.2.2.1 Simpangan Rata-Rata, Simpangan Rata-Rata Dari Data 3 4 6 7 8 8 Adalah, Cara Menentukan Simpangan Rata-Rata, Soal Simpangan Rata-Rata, Simpangan Rata-Rata Data Kelompok, Simpangan Rata-Rata Data Tunggal, Cara Menentukan Daftar Gaji Karyawan Indomaret – Umr, Ump Umk Terbaru 2022.
Hello Bestie Quipper Co Id, pada perjumpaan kali ini kembali akan mimin sampaikan pembahasan materi makalah tentang simpangan rata-rata.
Namun pada perjumpaan sebelumnya, yang mana mimin juga telah menyampaikan materi tentang Fungsi Kuadrat.
Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini maka, mari simak ulasan selengkapnya di bawah ini.
Daftar Isi :
Pengertian Simpangan Rata-Rata

Simpangan rata-rata ialah merupakan rata-rata suatu jarak antara nilai-nilai data yang akan menuju rata-ratanya.
Simpangan rata-rata merupakan masuk ke dalam ukuran penyebaran data seperti Varian dan Standar Deviasi.
Kegunaannya untuk mengetahui seberapa jauh nilai data yang telah ditemukan dari rata-rata yang telah diatur sebenarnya.
Rumus Simpangan Rata-Rata
Sekumpulan data kuantitatif yang tidak dapat di kelompok kan serta dapat di nyatakan dengan x1, x2, …, xn.
Dari data itulah dapat di hitung simpangan rata – rata (SR) dengan memakai rumus seperti di bawah ini :
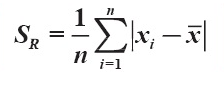
Simpangan Rata–Rata Data Tunggal
Rumus Variasi Data Tunggal
Rumus variasi atau sering disebut ragam dari data tunggal adalah yang dapat di nyatakan seperti dibawah ini :
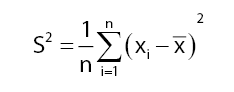
Keterangan :
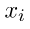
= nilai data ke-i
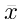
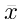
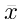
= rata – rata
n = jumlah seluruh frekuensi
Rumus Standar Deviasi/Simpangan Baku Data Tunggal
Rumus simpangan baku data tunggal dapat di nyatakan melalui sebuah persamaan seperti berikut :
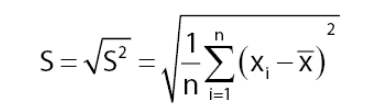
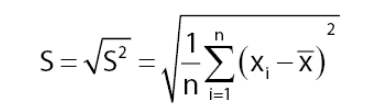
Keterangan :
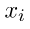
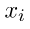
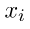
= nilai data ke-i
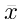
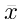
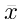
= rata – rata
n = jumlah seluruh frekuensi
Simpangan Rata–Rata Data Berkelompok
Rumus simpangn rata – rata (SR) data berkelompok seperti berikut :
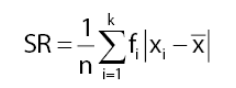
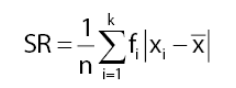
Keterangan :
n = jumlah seluruh frekuensi
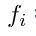
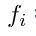
= frekuensi kelas ke-i
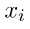
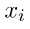
= nilai tengah kelas ke-i
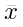
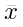
= rata – rata
k = banyaknya kelas interval
Variasi (Ragam)
Persamaan untuk ragam atau variasi dapat dikerjakan dengan rumus dibawah ini :
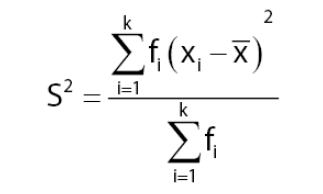
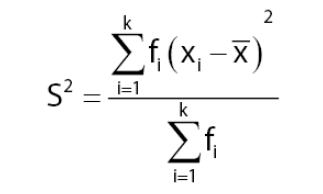
Keterangan :
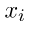
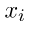
= nilai tengah kelas ke-i
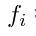
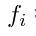
= frekuensi kelas ke-i
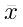
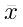
= rata – rata
k = banyak kelas interval
Standar Deviasi (Simpangan Baku)
Rumus simpangan baku untuk data kelompok adalah seperti berikut :
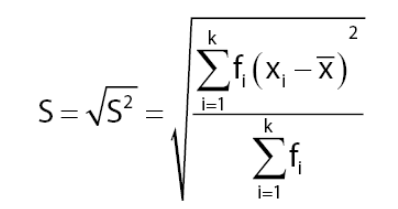
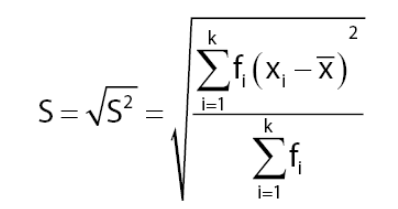
Keterangan :
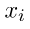
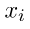
= nilai tengah kelas ke-i
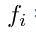
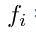
= frekuensi kelas ke-i
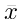
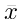
= rata – rata
k = banyak kelas interval
Soal Dan Pembahasan Simpangan Rata-Rata
1. Hitunglah simpaangan rata – rata nilai ulangan Akutansi siswa Kelas XI MAN 2 Bangsa seperti tabel dibawah ini :
Nilai ulangan Akutansi siswa Kelas XI MAN 2 Bangsa
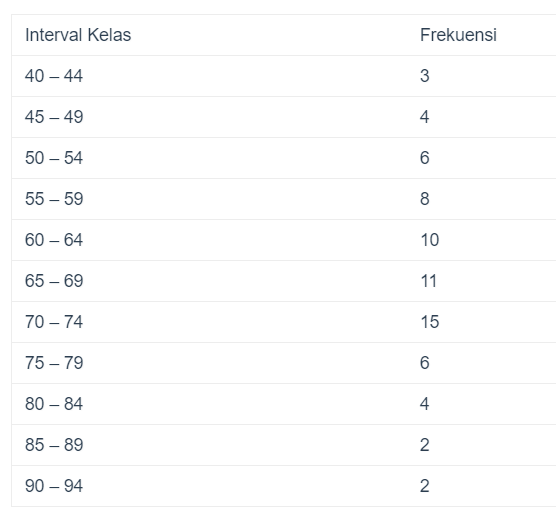

Penyelesaian :
Dari tabel diatas, didapatkan = 65,7 (telah di bulatkan).
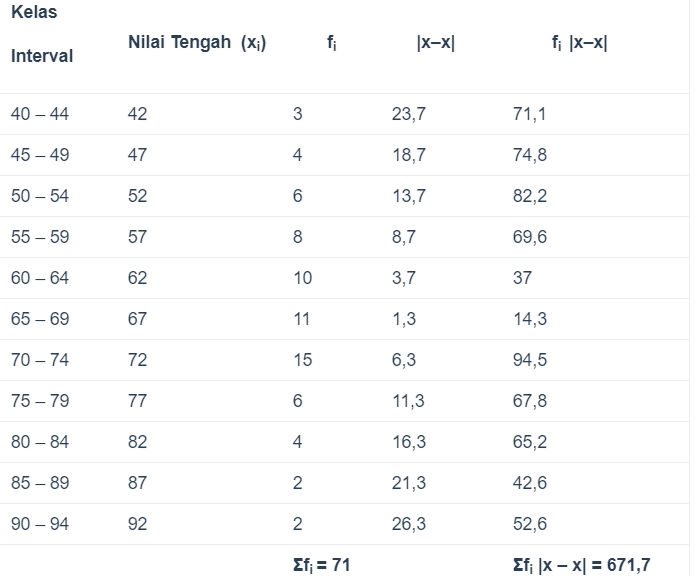

Maka, smpangan dari nilai rata – rata (SR) nilai ulangan Akutansi siswa Kelas XI MAN 2 Bangsa adalah = 671,7:71 = 9,46.
Perlu di ingat!!!
Simpangn rata – rataan hitung tersebut menunjuk kan rataan hitung jauh nya datum dari rataan hitung.
Supaya dapat menghitung simpangan baku data kuantitatif : 2,5,7,4,3,11,3 yaitu bisa menggunakan kalkulator ilmiah ( fx–3600Pv ) adalah sebagai berikut :
| 1) | Kalkulator “ON” | |
| 2) | MODE 3 → Program SD | |
| 3) | Masukkan data | |
| 2 data | ||
| 5 data | ||
| … | ||
| … | ||
| … | ||
| 3 data | ||
| 4) | Tekan tombol x αn-1 | |
| α = 2,878491669 = 2,88 |
2. Tentukan simpangan dari data Quantitatif seperti dibawah ini!
11,3,12,3,4,7,5,11
Penyelesaian :
Maka, simpangan nya yaitu 3,25
3. Hitunglah SR dari data Quantitatif berikut!
15, 3, 13,5,7,4,9, 21
Penyelesaian :
Maka, simpangaan rata-rata nya ialah 5,32.
4. Pada suatu sekumpulan data dapat dinyatakan dengan x1, x2, …, xn kemudian masing – masing nilai data tersebut memiliki frekuensi f1 , f2 , …, fn jadi dapat di perolehlah nilai simpangaan rata – rata (SR) dengan menggunakan rumus.
Hitunglah SR dari data berikut ini :
4,5,6, 777 8, 8, 9, 9
Penyelesaian :
Rata – ratanya ialah : = 7 SR
5. Pahamilah tabel data distribusi frekuensi dibawah ini :
| Nilai | Frekuensi |
| 11 – 15 16 – 20 21 – 25 26 – 30 31 – 35 | 2 2 10 9 4 |
Tentukan nilai SR data dari nilai di atas.
Penyelesain :
Temukan terlebih dulu titik tengah setiap kelas, untuk kemudian dicari nilai rata-rata nya :
| Nilai | Frekuensi | x |
| 11 – 15 16 – 20 21 – 25 26 – 30 31 – 35 | 2 2 10 9 4 | 13 18 23 28 33 |
Rata – ratanya ialah :


tapi pake titik tengah kelas dengan menggunakan x dapat diperoleh :
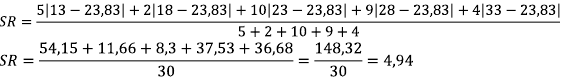
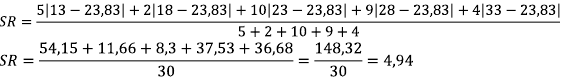
| xi | xi – | |
| 871011 | -1-212 | 1212 |
6. Dari tabel data yang diatas, diketahui rata – ratanya adalah 9. Carilah simpangn rata – ratanya!
Penyelesaian :
SR = 1,5
Aplikasi Pemecah Soal Matematika
Dijaman sekarang ini tidak heran kalau anak – anak lebih sering bertanya pada google dari pada bertanya pada orang tuanya.
Karena sekarang semua – semuanya bisa dicari digoole. Nah salah satu aplikasi yang baru saja di keluarkan oleh google play store adalah Qanda.
Qanda ini jenis aplikasi yang bisa membantu bestie menjawab soal – soal matematika dengan cepat, cara downloadnya mudah.
Bestie bisa mencarinya di google play store dengan mengetikan Aplikasi Qanda, atau juga bestie bisa langsung klik link ini.
Akhir Kata
Nah demikian materi yang dapat quipper.co.id sampaikan semoga dapat membantu teman – teman semua dalam memahami materi makalah tentang simpangan rata – rata. Semoga bermanfaat untuk kalian semua.
