Soal Latihan Matematika Kelas 5 SD – Nah pada perjumpaan kali ini akan quipper.co.id sampaikan materi pembahasan mengenai Soal Latihan Matematika Kelas 5 SD.
Sedangkan pada perjumpaan sebelumnya quipper.co.id sudah menjelaskan tentang materi 1 Sendok Makan Berapa Gram.
Sekarang untuk melengkapi isi dari tema pembahasan kita kali ini, maka simak ulasan selengkapnya di bawah ini.
Daftar Isi :
Kumpulan Soal Latihan Matematika Kelas 5 SD Semester 1 dan 2

Contoh soal matematika adalah kumpulan dari soal – soal yang sudah disusun dengan rapih dan bertujuan untuk bisa membantu anak – anak di dalam menjalankan aktifitas belajar mengajar yang materi nya disesuaikan dengan usia anak kelas 5 SD.
Contoh Soal Operasi Hitung
Bilangan Bulat
Bilangan bulat ialah merupakan sebuah bilangan yang terdiri dari kumpulan bilangan bulat positif, nol serta bilangan bulat negatife.
Contoh :
- Bilangan bulat positiv :
- 1,2,3,4, ….. seterusnya.
- Bilangan nol :
- 0
- Bilangan bulat negatif :
- -1, -2, -3, -4, ….. seterusnya.
Bilangan Cacah
Bilangan cacah ialah merupakan sebuah bilangan bulat positif yang dimulai dari angka 0 (nol) hingga hitungan tidak terhingga.
Contoh :
- 0, 1, 2, 3, 4, 5, ….. seterusnya
Bilangan Asli
Bilangan asli ialah merupakan sebuah bilangan bulat positif yang diawali oleh angka 1 (satu) hingga tidak terhingga.
Contoh :
- 1, 2, 3, 4, 5, ….. seterusnya.
Contoh Soal Sifat Komutatif
Sifat Komutatif Pada Penjumlahan
Contohnya :
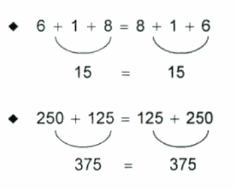
Maka rumus yang digunakan oleh sifat komutatif pada penjumlahan adalah :
| a+b=b+a |
Penjelasannya :
| Pertukaran pada suku dengan cara penjumlahan sama sekali tidak merubah hasilnya |
Sifat Komutatif Pada Perkalian
Contohnya :

screenshoot
Maka rumus yang digunakan oleh sifat komutatif pada perkalian adalah :
| axb=bxa |
Penjelasannya :
| Pertukaran dengan faktor pada perkalian tidaklah dapat merubah hasilnya |
Sifat Komutatif Tak Berlaku Dalam Pengurangan Serta Pembagian
Lihatlah!

Contoh Soal Sifat Asosiatif
Sifat Asosiatif Pada Penjumlahan
Contohnya :
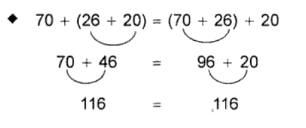
Maka rumus yang digunakan oleh sifat asosiatif pada penjumlahan adalah :
| a+(b+c)=(a+b)=c |
Penjelasannya :
| Penyatuan suku pada penjumlahan tidaklah dapat merubah hasilnya |
Sifat Asosiatif Pada Perkalian
Contohnya :
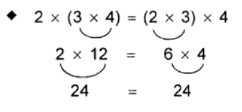
Maka rumus yang digunakan oleh sifat asosiatif pada perkalian adalah :
| ax(bxc)=(axb)xc |
Penjelasannya :
| Penyatuan faktor pada perkalian tidaklah merubah hasilnya |
Contoh Soal Sifat Distributif
Sifat Distributif Perkalian Dengan Penjumlahan
Contohnya :
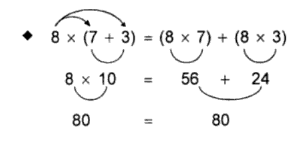
Maka rumus yang digunakan oleh sifat distributif pada perkalian dengan penjumlahan adalah:
| ax(b+c)=(axb)+(axc) |
Sifat Distributif Perkalian Dengan Pengurangan
Contohnya :
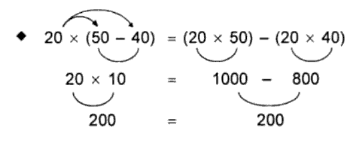
Maka rumus yang digunakan oleh sifat distributif perkalian dengan pengurangan adalah :
| ax(b-c)=(axb)-(axc) |
Contoh Soal Bilangan 0 (nol)
Bilangan 0 (nol) Adalah Bilangan Cacah
- Penjumlahan serta pengurangan dengan 0 (nol), hasilnya ialah merupakan bilangan itu sendiri ataupun tak berubah hasilnya.
Contohnya :
| 4+0=4 52+0=52 837+0=837 4328+0=4328 | 4-0=4 52-0=52 837-0=837 4328-0=4328 |
- Perkalian terhadap bilangan 0 (nol), hasilnya ialah merupakan 0 (nol).
Contohnya :
| 4×0=0 52×0=0 | 837×0=0 4328×0=0 |
Maka hasil dari bilangan berapapun yang dikalikan dengan 0 akan tetap sama yaitu 0 (nol).
- Pembagian pada bilangan 0, hasilnya yang tidak bisa didenfinisikan.
Contohnya :

Contoh Soal Bilangan 1 (satu)
Bilangan 1 Ialah Bilangan Cacah Dengan Bilangan Asli
- Perkalian serta pembagian dalam bilangan 1 (satu), akan menghasilkan bilangan itu sendiri.
Contohnya :
| 9×1=9 51×1=51 82×1=82 600×1=600 | 9:1=9 51:1=51 82:1=82 600:1=600 |
Maka hasil dari bilangan berapapun apabila di kalikan ataupun di bagi dengan angka 1, hasilnya tetap (tidak akan berubah).
Contoh Soal Pembulatan bilangan
Pembulatan Kepuluhan Terdekat
Peraturannya :
- Bila satuannya kurang dari 5, maka akan di bulatkan kebawah di anggap 0 (nol).
- Bila satuannya = 5 ataupun lebih, maka akan dibulatkan ke atas.
Contohnya :
| 33 dibulatkan menjadi 30 48 dibulatkan menjadi 50 56 dibulatkan menjadi 60 235 dibulatkan menjadi 240 534 dibulatkan menjadi 530 689 dibulatkan menjadi 690 |
Pembulatan Keratusan Terdekat
Peraturannya :
- Apabila puluhannya kurang dari 5, maka akan di bulatkan kebawah dianggap 0 atau bisa di hilangkan saja.
- Apabila puluhan = 5 ataupun lebih, maka akan di bulatkan keatas (di jadikan 100 genap).
Contohnya :
| 137 dibulatkan menjadi 100 174 dibulatkan menjadi 200 259 dibulatkan menjadi 200 261 dibulatkan menjadi 300 534 dibulatkan menjadi 500 689 dibulatkan menjadi 700 |
Pembulatan Kesatuan Terdekat Pada Pecahan Desimal
- Apabila angka dibelakang koma itu kurang dari 5, maka angka itu akan dihilangkan.
- Apabila angka di belakang koma = 5 atau bisa lebih, maka akan di bulatkan keatas.
Contohnya :
| 1,5 dibulatkan menjadi 2 2,6 dibulatkan menjadi 3 2,4 dibulatkan menjadi 2 3,9 dibulatkan menjadi 4 16,6 dibulatkan menjadi 17 28,3 dibulatkan menjadi 28 |
Contoh Soal Menaksir Operasi Hitung Bilangan
Menaksir Penjumlahan
Contoh Soal 1 :
Taksirlah penjumlahan berikut ini ke dalam satuan, menjadi puluhan serta ratusan terdekat.
| 3.772,5 + 2.594,1 = ….? |
Jawabannya :
| Taksiran kesatuan terdekat | 3.773 + 2.594= | 6.367 |
| Taksiran kepuluhan terdekat | 3.770 + 2.590= | 6.360 |
| Taksiran keratusan terdekat | 3.800 + 2.600= | 6.400 |
Contoh Soal 2 :
Taksirlah penjumlahan berikut ini menjadi taksiran rendah, taksiran tinggi dan juga taksiran baik pada ratusan.
| 553 + 293 = ….? |
Jawabannya :
| Taksiran rendah | 500+200= | 700 |
| Taksiran tinggi | 600+300= | 900 |
| Taksiran baik | 500+300= | 800 |
Contoh Soal 3 :
| 6.483+2.529=….? |
Jawabannya :
| Taksiran kepuluhan terdekat | 6.480+2.530= | 9.010 |
| Taksiran keratusan terdekat | 6.500+2.500= | 9.000 |
| Taksiran keribuan terdekat | 6.000+3.000= | 9.000 |
| Taksiran rendah | 6.000+2.000= | 8.000 |
| Taksiran tinggi | 7.000+3.000= | 9.000 |
| Taksiran baik | 6.000 + 3.000= | 9.000 |
| Hasil sebenarnya | 6.473+2.519= | 9.012 |
Taksiran baik adalah taksiran yang mendekati hasil sebenarnya.
Menaksir Pengurangan
Contoh Soal 1 :
Taksirlah pengurangan berikut ini ke satuan, puluhan, serta ratusan terdekat.
| 5.657,6-3.291,4=….? |
Jawabannya :
| Taksiran kesatuan terdekat | 5.658-3.291= | 2.367 |
| Taksiran kepuluhan terdekat | 5.650-3.2800= | 2.370 |
| Taksiran keratusan terdekat | 5.600-3.300= | 2.300 |
Contoh Soal 2 :
Taksirlah pengurangan berikut ini menjadi taksiran rendah, taksiran tinggi, serta taksiran baik.
| 682-399=….? |
Jawabannya :
| Taksiran rendah | 600-300= | 300 |
| Taksiran tinggi | 700-400= | 300 |
| Taksiran baik | 700-400= | 300 |
Contoh Soal 3 :
| 9.884-6.267=…..? |
Jawabannya :
Dikarenakan tidak ada koma maka tidak perlu ada taksiran kesatuan terdekat.
| Taksiran kepuluhan terdekat | 9.880-6.270= | 3.610 |
| Taksiran keratusan terdekat | 9.900-6.300= | 3.600 |
| Taksiran rendah | 9.000-6.000= | 3.000 |
| Taksiran tinggi | 10.000-7.000= | 3.000 |
| Taksiran baik | 10.000-6.000= | 4.000 |
| Hasil sebenarnya | 9.884-6.267= | 3.617 |
Menaksir Perkalian
Contohnya :
| 845×296=….? |
Jawabannya :
| Taksiran kesatuan terdekat | tidak ada | (tidak ada koma) |
| Taksiran kepuluhan terdekat | 850×300= | 255.000 |
| Taksiran keratusan terdekat | 800×300= | 240.000 |
| Taksiran rendah | 800×200= | 160.000 |
| Taksiran tinggi | 900×300= | 270.000 |
| Taksiran baik | 800×300= | 240.000 |
| Hasil sebenarnya | 845×296= | 250.120 |
Menaksir Pembagian
Contohnya :
| 792:334=….? |
Jawabannya :
| Taksiran kepuluhan terdekat | 790:330= | 2,5 |
| Taksiran keratusan terdekat | 800:300= | 3 |
| Taksiran rendah | 700:300= | 2,5 |
| Taksiran tinggi | 800:400= | 2 |
| Taksiran baik | 800:300= | 3 |
Kata Penutup
Nah demikian materi yang dapat quipper.co.id sampaikan semoga dapat membantu teman – teman semua dalam memahami materi makalah tentang Contoh Matematika Kelas 5 SD. Semoga bermanfaat untuk kalian semua.
Baca Juga : Contoh Soal Biologi Kelas 7 Semester 1 & 2 + Kunci Jawaban
