Bilangan Bulat – Hay sahabat semua.! Pada perjumpaan kali ini kembali akan quipper.co.id sampaikan pembahasan materi makalah tentang bilangan bulat.

Namun pada perjumpaan sebelumnya, yang mana kami juga telah menyampaikan materi tentang Angka Romawi. Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini maka, mari simak ulasan selengkapnya di bawah ini.

Daftar Isi :

Pengertian Bilangan Bulat

Bilangaan bulat merupakan sistem biilangan yang berupa himpunan dari semua biilangan dan bukan pecahan yang terdiri dari biilangan bulat negatif (…,-3,-2,-1), nol {0}, dan biilangan bulat positif (1,2,3,…). Bilangan bulat adalah himpunan bagian dari biilangan rasional.

Contoh bilangaan bulat positif:1, 2, 3, 4, . . .

Contoh biilangan nol:0

Contoh biilangan bulat negatif:-4, -3, -2, -1

Bilangan bulat dapat di tuliskan dan di urutkan dalam garis bilaangan. Penggunaan garis bilangan saat bermanfaat untuk melakukan operasi hitung biilangan bulat.

Biilangan bulat dapat di kelompokkan ke dalam dua bagian yaitu :

Bilangan genap:. . ., -6,-4,-2,0,2,4,6, . Biilangan genap adalah himpunan bilangan yang bila dibagi 2 menjadi 0.

Bilangan ganjil:. . .,-5,-3,-1,1,3,5, . Bilangan ganjil adalah himpunan biilangan yang bila dibagi 2 mejadi 1 atau -1.

Operasi Hitung Bilangan Bulat

Operasi hitung sederhana dalam biilangan bulat di antaranya ialah pengurangan, penjumlahan, pembagian, dan perkalian.

Sifat Dan Contoh Bilangan Bulat

Bilangan bulaat bisa ditulis dalam garis bilangaan sebagai berikut:

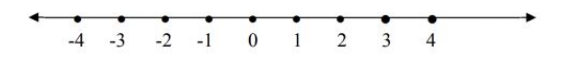
Dalam garis biilangan di atas, terdapat bilangan bulat yang dapat di kelompokkan dalam beberapa bagian.

Pengelompokan biilangan bulat seperti dibawah ini :

Sifat Asosiatif

Sifat asosiatif merupakan sifat pengelompokan. Sifat komutatif di tuliskan dengan (a+b)+c=a+(b+c).

Contoh :(4+7)+2=4+(7+2)=13

Sifat Komutatif

Sifat komutatif merupakan sifat pertukaran. Sifat komutatif ialah a+b=b+a. Contoh :5+8=8+5=13

Unsur Invers Terhadap Penjumlahan

Invers dari a ialah–a.

Invers dari –a ialah a.

Sifat invers dapat di tuliskan dengan a+(-a)=0.

Sifat Identitas Terhadap Penjumlahan

Unsur identitas terhadap operasi penjumlahan ialah biilangan 0.

Kenapa 0 di bilang sebagai unsur identitas terhadap penjumlahan?

Karena bila kita menghitung suatu biilangan dengan 0, hasil operasi penjumlahan akan tetap sama. Jadi dapat di tuliskan dengan 0+a=a+0. Contoh :8+0=0+8=8.

Operasi Pengurangan

Operasi pengurangan adalah operasi yang melibatkan tanda (– ). Dalam garis biilangan, suatu biilangan dapat di kurangi sama suatu bilangaan positif akan bergerak ke kiri.

Sifat – sifat dalam operasi pengurangan seperti di bawah ini :

a–b=a+(-b)

a–(-b)=a+b

Contoh :

3–1=3+(-1)=2

4–(-2)=4+2=6

Tidak berlaku sifat komutatif dan assosiatif :

a–b≠b–a

(a–b)–c≠a–(b–c)

Contoh :

4–2≠2–4

(6–2)–1≠6–(2–1)

Pengurangan yang melibatkan bilangaan 0 :

a–0=a dan 0–a=-a

Contoh :

4–0=4 dan 0–4=-4

Bersifat tertutup

Pengurangan yang melibatkan dua biilangan bulat, hasil operasi nya juga merupakan biilangan bulat.

Jika a dan b merupakan biilangan bulat, jadi a–b=c maka c merupakan bilaangan bulat.

Operasi Perkalian

Operasi perkalian ialah operasi matematika yang menggunakan tanda (×). Perkalian disebut sebagai penjumlahan yang berulang.

Perhatikan sifat-sifat operasi perkalian dibawah ini :

axb=ab adalah hasil perkalian dua bilaangan bulat positif yaitu biilangan bulat positif.

Contoh:5×6=30. 5,6,30 ialah merupakan biilangan bulat positif.

ax(-b)=-ab adalah hasil perkalian dari bilaangan bulat positif dan billangan bulat negative yang menghasil kan bilaangan bulat negatif.

Contoh: 3x(-4)=-12. Hasil operasi ialah -12 (bilangaann bulat negatif).

(-a)x(-b )=ab : adalah hasil dari perkalian dua biilangann bulat negatif merupakan bilangaan bulat positif.

Contoh: (-5)x(-2)=10, menghasilkan jumlah biilangan bulat positif yaitu 10.

Sifat komutatif

axb=bxa

Contoh:

9×2=2×9=18

Sifat assosiatif

(axb)xc=ax(bxc)

Contoh:

(3×2)x4=3x(2×4)=24

sifat distributif.

a x (b + c) = ab + ac

Contoh:

3 x ( 4 + 2) = (3 x 4) + (3 x 2) = 12 + 6 = 18

Unsur Identitas

Unsur identitas perkalian adalah 1. Perkalian suatu bilangaan dengan blangan 1 yang menghasilkan bilangan itu sendiri.

ax1=a

Contoh:

21×1=21.

Bersifat Tertutup

Jika a dan b bilangan bulat, menjadi axb=c yaitu c ialah merupakan bilangaan bulat.

Contoh:

7×2=14. ialah 7, 2, 14 merupakan blangan bulat.

Operasi Pembagian

Hasil bagi :

(+):(+)=(+)
(+):(-)=(-)
(-):(-)=(+)

Hasil bagi bilangaan bulat dengan 0 (nol) tidak terdefinisi.

a:0 = (tidak terdefinisi)

Contoh:

5:0 = (tidak terdefinisi)

Tidak berlaku sifat komutatif dan assosiatif.

a:b≠b:a
(a:b):c≠a:(b:c)

Contoh :

6:2≠2:6
(6:3):2≠6:(3:2)

Kesimpulan

Bilangaan ialah suatu konsep dalam matematika yang dipergunakan untuk mencari pencacahan dan pengukuran. Bilangan bulat ialah suatu bilangan pecahan yang terdiri dari bilangan bulat positif, nol, dan bilangan bulatt negatif.
Bilangaan bulat dapat di kelompok kan dalam beberapa bagian ialah bilangan bulat positif (1,2,3,4, .), bilaangan nol (0) , dan bilangann bulat negatif (,-4,-3,-2,-1).
Operasi sederhana dalam bilangaan bulat meliputi operasi penjumlahan, pengurangan, perkalian dan pembagian.

Nah Demikianlah yang dapat quipper co.id sampaikan kali ini tentang pembahasan mengenai materi makalah biilangan bulat. Semoga bermanfaat untuk teman-teman semua.