Belah Ketupat – Hay sahabat semua.! Pada perjumpaan kali ini kembali akan quipper.co.id sampaikan pembahasan materi makalah tentang belah ketupat.
Namun pada perjumpaan sebelumnya, yang mana kami juga telah menyampaikan materi tentang Bangun Datar. Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini maka, mari simak ulasan selengkapnya di bawah ini.
Daftar Isi :
Pengertian Belah Ketupat

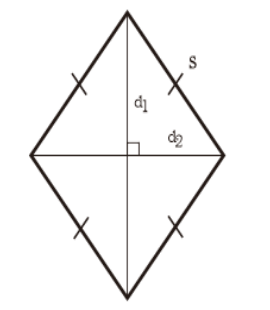
Belahh ketupatt adalah bangun datar 2 dimensi yang di bentuk dengan 4 buah sisi memiliki sama panjang dan memiliki 2 pasang sudut yang bukan siku – siku dan sudut yang sama – sama berhadapan memilikii besar yang sama. Dalam bahasa inggris blah ktupat disebut sebagai rhombus.
Rumus Belah Ketupat
| Nama | Rumus |
| keliling (Kll) | Kll = s + s + s + s |
| kll = s × 4 | |
| luas (L) | L = ½ × d1 × d2 |
| sisi (s) | s = Kll ÷ 4 |
| diagonal 1 ( d1 ) | d1 = 2 × L ÷ d2 |
| diagonal 2 (d2) | d2 = 2 × L ÷ d1 |
Sifat Belah Ketupat
1. Sudut yang saling berhadapan memiliki besar yang sama
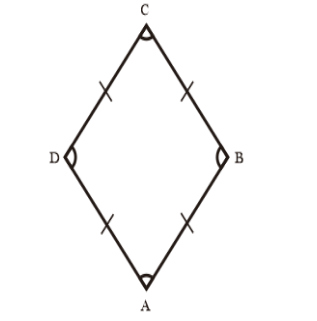
Pada belah ktupat sudut yang berhadapan mempunyai besar yang sama. Gambar di atas menunjuk kan besar sudut ∠ABC=∠ADC dan ∠BAD=∠BCD.
2. Besar keempat titik sudutnya 360º
3. Memiliki 2 Sumbu Simetri yang merupakan diagonal
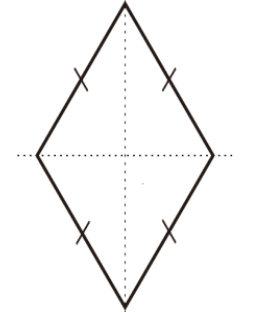
4. Memiliki 2 diagonal yang saling tegak lurus
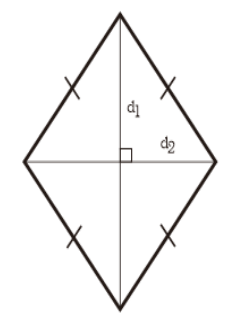
Diagonal 1 ( d1 ) dan diagonal 2 ( d2 ) pada belah ketupatt saling tegak lurus sehingga membentuk sudut siku – siku (90°).
5. Ke empat sisinya sama panjang
Jumlah Dua Sudut Yang Segaris
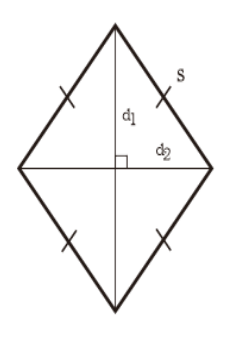
Dua sudut yang segaris pada gambar belah ketupaat diatas adalah :
- Sudut a sama sudut b,terletak pada garis ab.
- Sudut a sama sudut d,terletak pada garis ad.
- Sudut b sama sudut c,terletak pada garis bc.
- Sudut c sama sudut d,terletak pada garis cd.
Jadi ketika kedua sudut yang segaris ini di jumlahkan, maka menghasilkan 180⁰. Sama besar sudut lurus.
Luas Daerah Belah Ketupat
Untuk mencari luas sebuah daerah belah ketupat ABCD dengan mudah di cari dengan memakai rumus menghitung luas segitiga.
Luas dari belah ketupatt ABCD = luas segitiga ABD di tambah dengan luas segitiga CBD.
Luas belah ketupat ABCD
=Luas segitiga ABD+Luas segitiga CBD
=(1/2x BDxOA)+(1/2xBDxOC)
=1/2x(BDxOA)+( BDxOC)
=1/2x[(OA+OC)x BD]atau OA+OC= AC
Sampai,
Luas blah ktupat ABCD=1/2xACXBD
Dan, AC= diagonal 1 dan BD= diagonal 2.
Contoh Soal Belah Ketupat
Tentukan Luas
1. Jika AC= 10 cm, BD=6 cm
Tentukan luasnya!
Jawab:
Luas =½ xdiagonal1xdiagonal2
=½ x10 cmx6 cm
=30 cm2
2. Sebuah belaah ketupatt mempunyai diagonal 12 cm dan 14 cm .
Berapakah besar luasnya?
Jawab :
d1=12cm ,d2=14 cm
L=½ x d1xd2
=1/2 x12x14
L=84 cm2
Tentukan Diagonal
1. Jika luas belahh ketupaat ialah 96 cm2 dan diagonal 1 adalah 12 cm. Tentukan diagonal 2 nya!
Jawab:
L = ½ x diagonal1 xdiagonal2
96 cm2 = ½ x 12cmx d2
96 cm2 = 6cm x d2
d2 =16cm
Sifat (Teorema)
Semua sisi setiap belahh ketupatt sama panjang.
Pembuktian :
Belahh ketupatt ABCD di bentuk dari dua buah segitiga sama kaki yang kongruen, ialah ∆ABC dan ∆ADC.
∆ ABC ∆ ADC
AB=AD
BC=CD KONGRUEN (ss,ss,ss)
AC=AC
∆ABC sama kaki, jadi
AB=BC
∆ADC sama kaki, jadi
CD=AD
Maka:AB=AD=DC=AD ( Terbukti )
Setiap Blah Ktupat diagonalnya merupakan sumbu simetri.
Pembuktian :
- ∆ABC sama kaki dengan AB=CB, BO ialah sumbu simetri.
- ∆ADC sama kaki dengan AD= DC,DO ialah sumbu simetri.
- <BOC dan< COD berpelurus , jadi BD ialah sumbu simetri.
- < BOC dan< BOA berpelurus, jadi AC ialah sumbu simetri.
- Jadi terbukti BD dan AC ialah sumbu simetri.
- Pada setiap belahh ketupt sudut berhadapan nya sama besar dan dapat di bagi sama besar oleh diagonal – diagonal nya
Pembuktian :
Cara I
- Letak belah ketupatt ABCD di balik merupakan simetri BD
Maka< A→< C menjadi :
< A=< C ….. (1)
- Letak belahh ketupaatt ABCD di balik merupakan sumbu simetri AC jadi < B→< D menjadi <B =< D ….. (2)
- Dari (1) dan (2), jadi :
<A=<C, <B=<D ( Terbukti )
Cara II
- < A1 = < C2 (berseberangan dalam) → BO = DO
- < A2 = < C1 (berseberangan dalam) → DO = BO
- < B1 = < D2 (berseberangan dalam) → AO = CO
- < B2 = < D1 (berseberangan dalam) → CO = AO
- < AOB = < AOD = < AOD = < COD = 90o (siku)
- < BOD = 180o (lurus)
- < AOC = 180o (lurus)
- < COD = < AOD = 90o
- < BOD = < AOB + < AOD = 2 x < AOB = 2 x 90o = 180o
- < AOC = < AOD + < COD = 2 x < AOD = 2 x 90o = 180o
Jadi, AC dan BD merupakan diagonal ketupatt yang sama – sama membagi dua sama panjang dan saling berpotongan tegak lurus.
Kata Penutup
Nah demikian materi yang dapat quipper.co.id sampaikan semoga dapat membantu teman-teman semua dalam memahami materi makalah tentang belah ketupat.
Baca Juga :
