Aturan Sinus Dan Cosinus – Hay sahabat semua.! Pada perjumpaan kali ini kembali akan quipper.co.id sampaikan pembahasan materi makalah tentang aturan sinus dan cosinus. Namun pada perjumpaan sebelumnya, yang mana kami juga telah menyampaikan materi tentang Bangun Datar. Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini maka, mari simak ulasan selengkapnya di bawah ini.

Daftar Isi :

Pengertian Aturan Sinus

Aturan sinus adalah perbandingan antara panjang sisi segitiga dengan sinus menghadap nya yang memiliki nilai sama.

Untuk lebih jelasnya, perhatikan gambar dibawah ini :

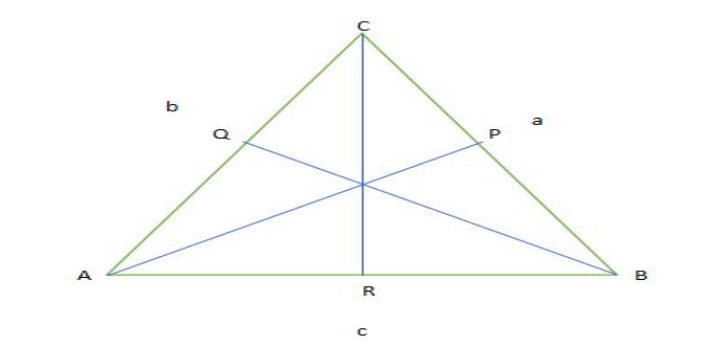
Keterangan Sinus :

A= Jumlah besar sudut pada hadapan si sisi a
a=Panjang sisi a
B= Jumlah besar sudut pada hadapan si sisi b
b=Panjang sisi b
C= Jumlah besar sudut pada hadapan si sisi c
c=Panjang sisi c
AP┴BC
BQ┴AC
CR┴AB

Perhatikan baik – baik segitiga ACR :

Sin A=^CR/b jadi CR=b sin A …(1)

Perhatikan baik – baik segitiga BCR :

Sin B=^CR/_{_a} jadi CR=a sin B …. (2)

Perhatikan baik – baik segitiga ABP :

Sin B=^AP/ jadi AP= C sin B … (3)

Perhatikan baik – baik segitiga APC :

Sin C=^AP/_b jadi AP=b sin C …(4)

Berdasarkan persamaan (1) dan (2) di peroleh :

CR =b sin A= a sin B jadi ^a/_{sin A}= ^b/_{sin B} …(5)

Berdasarkan persamaan (3) dan (4) di peroleh :

AP =c sin B=b sin C jadi ^b/_{sin B}=^c/_{sin C} …(6)

Berdasarkan persamaan (5) dan (6) di peroleh :

^a/_{sin A}= ^b/_{sin B}=^c/_{sin C}

Persamaan ini adalah yang dimaksud dengan aturan sinus.

Pengertian Aturan Cosinus

Aturan cosinus adalah aturan yang menceritakan hubungan antara kuadrat panjang pada sisi dan nilai cosinus dari satu sudut segitiga.

Untuk Lebih jelasnya, perhatikan gambar dibawah ini :

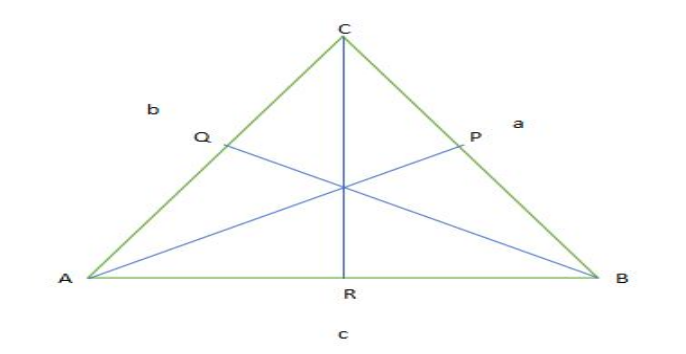
Keterangan Cosinus :

A=Besar sudut hadapan sisi a
a=Panjang sisi a
B=Besar sudut hadapan sisi b
b=Panjang sisi b
C=Besar sudut di hadapan sisi c
c=Panjang sisi c
AP┴BC
BQ┴AC
CR┴AB

Perhatikan baik – baik segitiga BCR :

Sin B=^CR/_{_a} jadi CR=a sin B

Cos B=^BR/_{_a} jadi BR=a cos B

AR =AB–BR=c–acosB

Perhatikan baik – baik segitiga ACR :

b² =AR²+CR²

b² =(c–a cos B)²+(a sin B)²

b² =c²–2ac cos B+a² cos² B+a² sin²B

b² =c²–2ac cos B+a²(cos² B+sin² B)

b² =c²+a²–2ac cos B

Memakai analogi yang sama, kemudian di peroleh aturan cosinus untuk segitiga ABC seperti di bawah ini :

a²=c²+b²–2bc cosA

b² =a²+c²–2ac cosB

c² =a²+b²–2ab cosC

Contoh Soal Sinus

Tentukan Luas Dari Segitiga ABC

1. Diketahui sebuah segitiga ABC dengan panjang AB=9cm dan BC=12cm. Jika besar ∠ ABC=30^o.

Tentukan luas segitiga ABC!

Penyelesaian :

L = ½ a t

Contoh a=AB, jadi t ialah garis tegak lurus AB ke titik C berhadapan dengan ∠ ABC, maka :

Sin ∠ABC=^t/_BC

t =BC×Sin∠ABC

Hasil yang di dapat :

L=½at

L=½×AB×BC×Sin∠ABC

L=½×9cm×12cm×Sin30^o

L=½×9cm×12cm×½

L=27cm²

Contoh a=BC, jadi t adalah garis tegak lurus BC ke titik A berhadapan dengan ∠ ABC, jadi :

Sin∠ABC=^t/_AB

t =AB×Sin∠ABC

Sehingga memperoleh :

L=½ at

L=½×BC×AB×Sin∠ABC

L=½×12cm×9cm×Sin30^o

L=½×12cm×9cm× ½

L= 27cm²

Maka, hasil yang di dapat luas segitiga ABC adalah 27cm².

Tentukan Besar ∠ABC Dari Segitiga ABC

2. Diketahui sebuah segitiga ABC mempunyai luas sebesar 6cm². Jika panjang AB=3cm dan BC=4cm.

Tentukan besar ∠ABC!

Penyelesaian :

L=½×AB×BC×Sin ∠ABC

6cm²=½×3cm×4cm×Sin ∠ABC

6cm²=6cm²×Sin ∠ABC

Sin∠ABC=1

ABC=arcsin (1)

ABC=90^o

Maka, besar ∠ABC adalah 90^o.

Contoh Soal Cosinus

Tentukan Panjang Sisi b Pada Segitiga ABC

1. Diketahui segitiga ABC mempunyai sisi dengan panjang :

a=10 cm

c=12 cm

besar sudut B=60̊.

Tentukan panjang sisi pada b!

Penyelesaian :

b²=a²+c²–2ac cos B

b²=100+144 – 44 cos 60̊

b²=244 – 44(0,5)

b²=244–22

b²=222

b=14,8997

Maka, panjang sisi pada b adalah 14,8997 cm.

Nah demikian materi yang dapat quipper.co.id sampaikan semoga dapat membantu teman-teman semua dalam memahami materi tentang aturan sinus dan cosinus ini.