Bilangan Eksponen – Hay sahabat semua.! Pada perjumpaan kali ini kembali akan quipper.co.id sampaikan pembahasan materi makalah tentang bilangan eksponen. Namun pada perjumpaan sebelumnya, yang mana kami juga telah menyampaikan materi makalah tentang Angka Romawi. Nah untuk melengkapi apa yang menjadi pembahasan kita kali ini, maka mari simak ulasan selengkapnya di bawah ini.

Daftar Isi :

Pengertian Bilangan Eksponen

Eksponen merupakan suatu bentuk bilangan dari perkalian yang memiliki bilangan yang sama, dan dapat diulang kembali atau pengertian singkat nya ialah suatu perkalian yang dapat di ulang-ulang.

Bilangan eksponen biasanya di gunakan lebih luas di berbagai bidang yang ada. Contohnya biologi,kimia,fisika,dan ilmu komputer.

Fungsi Eksponen Dan Grafik

Fungsi eksponen ialah fungsi pemetaan dalam bilangan yang real x pada bilangan ax dengan a>0 dan a≠

Apabila a>dan a≠1, x∈R jadi fLx) = ax disebut fungsi eksponen.

Fungsi eksponen,y=f(x)=ax:a>0 dan a ≠1 memiliki sifat-sifat seperti dibawah ini :

Kurva terletak pada atas sumbu x yang mempunyai nilai positif.
Memotong pada sumbu y dalam titik 0,1.
Memiliki asimtot yang datar y=0 sumbu x. Arti dari asimtot ini ialah garis sejajar dengan sumbu x.
Grafik monoton yang naik pada bilangan x>1.
Grafik monoton yang turun dalam bilangan 0<x<1

Rumus Persamaan Eksponen

Bentuk persamaan eksponen merupakan persamaan yang terdapat beberapa pangkat dalam bentuk sebagai fungsi x yang mana x ialah sebagai bilangan peubah.

Sifat Bilangan Eksponen

Pertama :

a^mxaⁿ = n^m+n(apa bila di kali maka pangkat nya akan di tambah)

Contoh : 6²x6³=6²⁺³=6⁵

Kedua :

a^m:aⁿ=a^m–n(apa bila di bagi maka sebalik nya pangkat nya harus di kurang)

Contoh : 8⁵:8³=8^{5 – 3}=8²

Ketiga :

(a^m)ⁿ=a^mxn(apa bila di dalam kurung maka pangka tnya harus di kalikan)

Contoh : (9²)³=9^{2 x 3}=9⁶

Keempat :

(axb)^m=a^mxb^m

Contoh : (4×5)²=4².5²

Kelima :

Sifat yang ke lima , memiliki syarat “b”atau penyebut b tidak boleh sama dengan nol (0).

(a/b)^m = a^m/b^m

Contoh :

(5/3)² = 5²/3²

Ke enam :

Pada sifat yang ke enam, apabila (aⁿ) di bawah nya bilangan positif, jadi saat di pindahkan ke atas berubah menjadi bilangan negatif. Begitu juga sebalik nya, apabila(aⁿ) di bawah nya adalah bilangan negatif, maka saat di pindahkan ke atas otomatis berubah menjadi bilangan positif.

Perhatikan rumus di bawah ini :

Ke tujuh :

Pada sifat yang ke tujuh, kita bisa lihat bahwa terdapat akar pada ⁿ dari a^m. Ketika di sederhanakan, maka akar pada ⁿ akan menjadi penyebut dalam blangan dan akar ^m menjadi penyebut pembilang.

Bersamaan syarat ⁿ wajib lebih besar atau = 2.

Contohnya rumus di bawah ini :

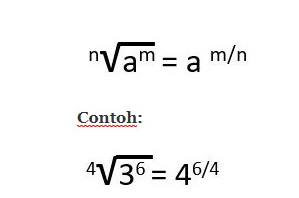
Ke – 8 :

Bilangan eksponen nol sama persis dengan a=1.

Contohnya :

4=1

8=1

11=1

Memiliki syarat a tidak boleh sama dengan nol.

Bentuk Bilangan Eksponen

Bilangan Eksponen Negatif

Apabila M dan N ialah bilangan bulat positif jadi :
a^-n=1/aⁿ
Contoh :
3^-4=1/3⁴=1/81

Bilangan Eksponen Pecahan

Rumus : a^1/n = ⁿ√a

Contoh :
2^1/2=√2
2^1/3=³√2

Bilangan Eksponen Nol (0)

Apabila a≠0 jadi a=1 atau a tidak boleh sama dengan hasil 0.

contoh:
5=1
9=1
99 =1
y=1

Rumus Persamaan Eksponen

Bentuk persamaan eksponen merupakan persamaan yang terdapat beberapa pangkat dalam bentuk sebagai fungsi x yang mana x ialah sebagai bilangan peubah.

Rumus :

Af(X) =1(Apabila AF(X)=1 dengan A>0 dan A ≠0, jadi F (X)=0)
AF(X =AF(Apabila AF(x)= AP dengan A>0 dan A≠0, jadi F(X)=P)
AF(X)= AG(X) (Apabila AF(X)=AG(X) dengan A>0 dan A≠0,jadi F(X) = G(X))
AF(X)=BF(X) (Apabila AF(X)=BF(X) dengan A>0 dan A≠1, B>0 dan B ≠1, dan A≠B jadi F(X)=0)
A(AF(X))2+B(AF(X))+C=0 (Dengan AF(X)= P, jadi bentuk persamaan dapat dirubah menjadi persamaan kuadrat: AP2+BP+C=0)

Contoh Soal Eksponen

1. Tentukan hasil dari :

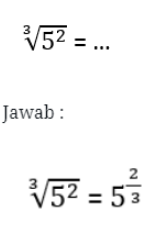
2. Bentuk sederhana dari soal dibawah ini!

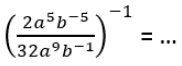
Jawab :
Dengan menerapkan sifat eksponen ke-3 :

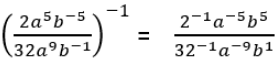
3. Dengan menerapkan sifat eksponen ke-5 :

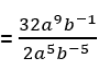
= 16 a^(9-5) b^{(-1- (-5))}
= 16a⁴b⁴ = (2ab)⁴

4. Soal

Jika 3^{x -2y}= 1/81 dan 2^x-y = 16

maka nilai x+y = . . .

Pembahasan :
Persamaan 1 :
3^{x -2y}=1/81
3^x-2y=81 ^-1
3^x-2y=(3⁴)^-1
x-2y=-4 …. (i)

Persamaan 2 :
2^x-y=16
2^x-y=2⁴
x-y=4 …. (ii)

Dari persamaan 1 dan 2, mendapatkan hasil :

(i) x – 2y = -4
(ii) x – y = 4
Dikurangi jadi hasilnya -y = -8
y = 8 dan x = 12
Sehingga nilai dari x = y = 12 + 8 = 20

Nah Demikianlah yang dapat quipper.co.id sampaikan kali ini tentang pembahasan mengenai materi tentang bilangan eksponen. Semoga bermanfaat untuk teman-teman semua.