Materi Distribusi Normal – Hay sahabat semua.! admin Balik lagi pada kesempatan kali ini dan akan menyampaikan pembahasan materi matematika tentang Distribusi Normal.
Materi matematika adalah salah satu materi pelajaran yang banyak disukai oleh semua kalangan yang ada diseluruh dunia, khusunya indonesia.
Tapi masuh inget gak, di pertemuan – pertemuan sebelumnya, admin juga udah banyak menjelaskan tentang beberapa materi matematika salah satunya tentang Bilangan Desimal.
Nah biar sahabat gak kelamaan nungguin materi yang akan admin sampaikan, yuk langsung di simak aja uraian selengkapnya seperti yang sudah admin sediain di bawah ini.
Daftar Isi :
Pengertian Distribusi Normal

Distribusi normal merupakan distribusi dari suatu variabel acak yang berkelanjutan. Biasanya juga distribusi normal sering dinamakan sebagai pengertian distribusi Gauss.
Distribusi ini merupakan distribussi yang paling penting dan paling banyak digunakan di bidang statistika.
Abraham de Moivre lah yang memperkenalkan tentang Distribusi normal untuk pertama kali di dunia di dalam suatu artikel miliknya pada tahun 1733 sebagai pendekatan distribussi binomial untuk (n) besar.
Kemudian karya itu dimajukan menjadi lebih baik lagi oleh Pierre Simon de Laplace Dan dikenal sebagai teorema Moivre-Laplace.
Laplace memanfaatkan distriibusi normal untuk membantu menganalisis galat suatu eksperimen.
Rumus Distribusi Normal
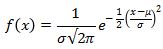
Keterangan :
- π : Konstanta dengan nilai 3,14159. . . .
- e : Bilangan eksponensial dengan nilai 2,7183 . . . .
- µ : Rata-rata (mean) dari data
- σ : Simpangan baku data berdistribusi normal
Cara Menghitung Nilai Z.
z = (x – µ)/σ
Keterangan:
- µ : Rata-rata (mean) dari data
- σ : Simpangan baku data berdistribusi normal
Akan tetapi, Kita dapat lebih mudah dengan menggunakan bantuan tabel distribusi normal.
Berikut merupakan tabel distribusi normal standar.
Untuk P ( X < x ) atau dapat digambarkan dengan luas kurva normal standar dari X = minus tak terhingga
sampai dengan X = x
Ciri Ciri Distribusi Normal
Berikut adalah ciri dari distribussi yang perlu sobat ketahui:
- Mempunyai sebuah parameter µ dan σ yang lokasi serta bentuk distribusinya dapat ditentukan sendiri.
- Kurva juga memiliki suatu puncak tunggal
- Rata-rata terletak di tengah distribusi dan distribusinya simetris di sekitar garis tegaklurus yang ditarik melalui rata-rata
- Total luas daerah di bawah kurva normal adala 1 (hal ini berlaku untuk seluruhdistribuso probabilitas kontinu
- Dapat memotong sumbu horizontal dan dapat memanjang kedua ekor kurva itu hingga tidak ada batasnya.
- Kurvanya berbentuk seperti lonceng atau genta
- Standar deviasi σ (Simpangan baku) yang menjadi penentu lebarnya kurva. Akan semakin runcing bentuk kurvanya apabila makin kecil σ.
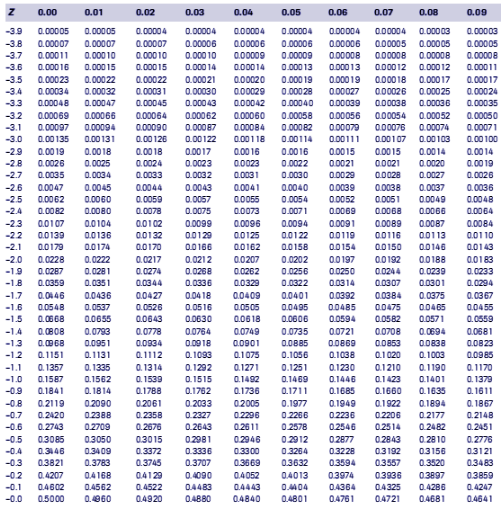
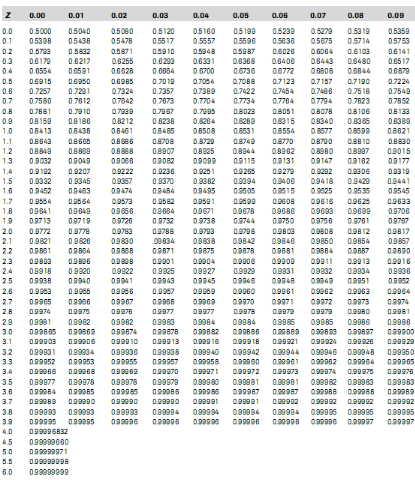
Tabel Distribusi Normal
Contoh Soal Distribusi Normal
Soal Latihan Nomor 1
Rata-rata produktivitas padi di lampung tahun 2009 adalah 6 ton per hektare (ha), dengan simpangan baku (s) 0,9 ton .
Apabila luasnya sawah yang di Lampung 100.000 hektare (ha) dan produktivitas padi berdistribusi normal (data tentatif), tentukan berikut ini!.
- jadi berapakah luasnya sawah yang memiliki produktivitas yang lebih dari 8ton ?
- jadi berapakah luasnya sawah yang memiliki produktivitas yang kurang dari 5ton ?
- jadi berapakah luasnya sawah yang memiliki produktivitas diantara 4–7ton ?
Keingintahuan tentang diatas tersebut dapat kita jawab beserta memanfaatkan beberapa sifat distribussi normal seperti yang telah ditetatpkan pada Tabel Z.
1. Jumlahkan nilai z dari nilai x= 8 ton dengan menggunakan rumus
![clip_image002[10]](https://hatta2stat.files.wordpress.com/2011/11/clip_image00210_thumb.gif?w=213&h=35)
2. Jumlahkan nilai z dari nilai x= 7 ton, dengan menggunakan rumus
![clip_image002[3]](https://hatta2stat.files.wordpress.com/2011/11/clip_image0023_thumb.gif?w=213&h=35)
3. Jumlahkan luasnya dibawah kurva normal terhadap z=–2,22.
Langkah pertama bukalah Tabel Z serta lihatlah sel di tengah- tengah baris 2, 20 serta kolom 0, 02. Jumlahnya ialah angka 0,01321 dan jika dijadikan persen menjadi 1,321%.
Angka ini menunjukkan bahwa luasnya dibawah kurva normal baku dari titik –2,22 arahkan menuju kiri kurva ialah sejumlah 1,321%.
4. Jumlahkan luasnya dibawah kurva normal terhadap z = 1,11.
Langkah pertama bukalah Tabel Z serta lihatlah sel di tengah- tengah baris 1,10 serta kolom 0,01. Jumlahnya ialah angka 0,86650 dan jika dijadikan persen menjadi 86,65%.
Angka ini menunjukkan bahwa luasnya dibawah kurva normal baku dari titik 1,11 arahkan menuju kiri kurva ialah sejumlah 86,65%.
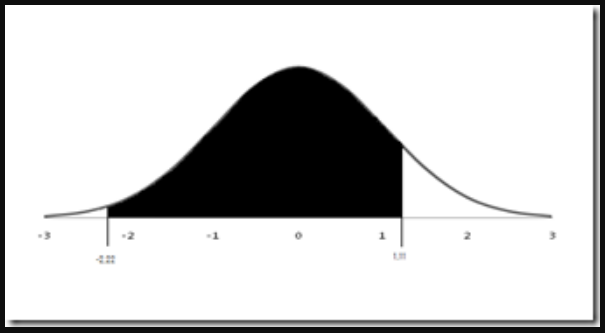
5. Luas sawah yang produktivitasnya antara 4 – 7 ton
Adalah 86,65%-1,321% = 85,329% (diarsir dengan berwarna hitam) atau (85,329/100) x 100.000 ha = 85329 ha (hektare). seperti gambar dibawah.
Soal Latihan Nomor 2
2. Contohnya apabila kita menentukan 20saham di bulan Mei 2007.
Harga saham ke- (20) pada perusahaan itu sekitar-Rp. 2000 – 2805 dalam satu lembarnya.
Tahukah probabilitasnya harga saham itu di antara Rp. 2500 sampai 2805 dalam satu lembarnya.
Diketahui μ = 2500 untuk jumlah nilai rata-ratanya dalam hitungan dan 400 jumlah deviasi standarnya.
jawab :
Z = (X – μ) / σZ1 = (2500 – 2500) / 400 Z1 = 0 / 400 = 0 Z2 = (2805 – 2.805) / 400Z2 = 0.76
Soal Latihan Nomor 3
Telah ditemukan harga rata- ratanya dari 100 responden sebagai angket motivasi kerja =75 dengan simpangan baku = 4
ditanyakan:
- 1.Berapakah total respondennya yang mendapat nilai 80 keatas?
- 2.Berapa nilai responden yang dapat dikualifikasikan 10 % dari nilai tertinggi?
Jawaban :
- 1. Z = (80 –75)/4 = 1,25 dari tabel kurva normal didapat luas kekanan = 10,56 %. Maka hasil responden = 10,56%x100= 11 orang
- 2. Batas kualifikasi 10% tertinggi = 50 % – 10 % = 40 % dari tabel maka diperoleh 1,28. karena SD tertinggi 4, maka untuk 1,28 SD = 1,28 x 4 = 5,12. jadiskortertinggi= 75 + 5,12 = 80,12
Soal Latihan Nomor 4
Santo ialah seorang yang berdagan buah di lampung tengah. Hampir setiap saat ia selalu memborong sekitar 300 kg buah di Tanjung Karang Bandar Lampung.
Untuk jumlah probabilitas buah itu yang mampu terjual ialah sebebsar 80% beserta 20%nya dapat saja menjadi tidak terjual atau membusuk.
Tahukah jumlah probabilitas buah apabila terdapat 250kg yang terjual serta tidak membusuk ?
Jawab :
- = 300; probabilitas laku p = 0.8, dan q = 1 – 0.8 = 0.2μ
- = np = 300 x 0.80 = 240
- σ = √npq = √300 x 0.80 x 0.20 = 6.93
- Diketahui X = 250, dan dikurangi faktor koreksi 0.5 sehingga X = 250 – 0.5 = 249.5
- Maka saat ini nilai Z akan berubah jadi:
- Z = (249.5 – 240) / 6.93 = 1.37 dan P (Z<1.37) = 0.4147
- Maka probabilitas yang terjual ialah 0.5+0.4147=0.9147
- Perkiraan buah laku di dalam 250 kg adalah 91.47%
Demikianlah materi pembahasan kali ini yang dapat quipper.co.id sampaikan mengenai distribussi normal, semoga ulasan ini bisa bermanfaat untuk teman-teman semua.
