Materi Fungsi Komposisi – Hay sahabat semua pada perjumpaan kali ini kembali akan kami sampaikan pembahasan mengenai fungsi komposisi.
Namun pada perjumpaan sebelumnya kami juga telah menyampaikan materi tentang Operasi Aritmatika Nah untuk lebih jelasnya, bisa sobat simak ulasan selengkapnya di bawah ini.
Daftar Isi :
Pengertian Fungsi Komposisi

Apa Yang dimaksud dengan Fungsi komposisi? yakni merupakan suatu perpaduan atas sebuah operasi yang terkait dengan 2 jenis fungsi f (x) dan g (x) hingga kemudian akan dapat memperoleh hasil fungsi yang baru.
Rumus Fungsi Komposisi
Pada dasarnya rumus fungsi kompossi itu pengertiannya dibagi menjadi 2fungsi antara lain seperti yang dijelaskan dibawah ini :
fungsi f(x) dan fungsi g(x), jadi fungsi h(x) yang dijabarkan sebagai fungsi h(x)=(f o g)(x) bisa ditemukan dengan cara seperti contoh dibawah ini :
h(x) = (f o g)(x) = f(g(x))
Misalkan contoh prakteknya ialah Apabila ditemukan adanya fungsi f dan g yang menandakan mesin itu berkerja dengan cara saling beriringan.
Fungsi g memperoleh input yaitu (x) yang telah dikerjakan dengan mesin f dan selanjutnya output menjadi g(x).
Lalu g(x) dijadikan sebagai input untuk dapat diproses oleh mesin f sehingga menjadi outputnya yaitu f(g(x)).
Komposisi Fungsi
Pada komposisi fungsi ini telah ditemukan akan adanya istilah lain tentang fungsi komposisi yang wajib di ketahui, bahwa pengertian itu adalah kompossi fungsi.
Komposisi fungsi merupakan hasil dari penyatuan operasi melalui dua fungsi yang bergantian sehingga menemukan sebuah fungsi baru.
Sebagai notasinya, notasi tersebut dihasilkan oleh komposisi fungsi yang mempunyai kesamaan dengan notasi fungsi kompossi yaitu ‘o’ atau ‘bundaran’.
Sifat dari Komposisi Fungsi
Terdiri dari beberapa sifat dari kompossi fungsi, penjelasannya seperti dibawah ini :
- Tidak memiliki sifat komutatif yaitu (f o g)(x) ≠(g o f)(x)
- Memiliki sifat assosiatif yaitu ((f o g) o h)(x) = (f o (g o h))(x)
- Dan bila fungsi identitas I(x), maka akan menjadi (f o l)(x) = (l o f)(x) = f(x).
Fungsi Komposisi pada Kehidupan
Pengertian dari fungsi komposisi pada kehidupan itu memiliki contoh fungsi kompossi yang terdapat di kehidupan sehari-hari, penjelasannya seperti di bawah ini :
1. Melalui proses memproduksi buku dapat dilakukan dengan dua langkah, yaitu :
- Langkah pertama- tama adalah editing dan selanjutnya akan langsung ke langkah produksi.
- Di saat melakukan langkah editing, naskah itu akan segera di edit dan di layout untuk berubah sebagai file yang sudah sangat siap dicetak.
- Selanjutnya, file dapat segera diproses ke langkah produksi percetakan agar dapat 100% menjadi sebuah buku.
- Proses produksi buku ini ialah memakai penerapan dari algoritma fungsi komposisi.
2. Sebagai proses mendaur ulang logam yaitu :
- Untuk proses awalnya beberapa pecahan logam campuran akan dijadikan satu agar dapat menjadi sebuah serpihan kecil.
- Selanjutnya Drum magnetic yang berada di dalamnya mesin penghancur itu dapat membedakan logam magnetic yang memiliki unsur besi dengan unsur lainnya.
- Berikutnya sisa dari pecahan logam tersebut dikeruk serta dilakukan pemisahan. Dan untuk serpihan besi dapat segera dilebur menjadi baja baru. Proses pendauran ulang logam ini merupakan menggunakan penerapan fungsi komposisi.
Fungsi Invers
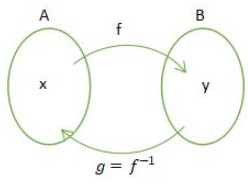
Dijelaskan fungsi f adalah fungsi yang memetakan dari A ke B serta mempunyai relasi dengan fungsi g yang memetakan B ke A, jadi fungsi g adalah invers atau kebalikannya dari f dan ditulis f-1 atau g = f-1. Apabila g adalah fungsi, maka g = f-1 dapat dinamakan fungsi invers atau fungsi balikan.
Agar dapat lebih memahaminya, maka lihatlah gambar di bawah ini :
Cara Mencari Invers dari Suatu Fungsi
Cara mencari invers dari suatu fungsi ialah misalnya, fungsi y=f(x) bisa diketahui melalui cara di bawah ini:
- Buatlah perubahan dalam persamaan y=f(x) ke dalam bentuk x=f(y).
- Lalu rubahlah x dengan f-1(y) sehingga menjadi f(y) = f-1(y).
- Apabila y dengan x dirubah, maka akan ditemukan invers dari f(x) berupa f-1.
Contoh Soal Fungsi Komposisi
1. Apabila ada sebuah fungsi f(x)=5x+1 dan diperoleh bahwa (f o g) (x) = 10x+6 jadi g(x) ialah?
Pembahasan :
- (f o g)(x) = 10x + 6
- f(g(x)) = 10x + 6
- 5(g(x))+1 = 10x + 6
- 5(g(x)) = 10x + 5
- g(x) = 2x + 1
Apabila fungsi g(x) yang dicari ialah g(x) = 2x + 1
2. Dengan menggunakan soal No.1, maka tentukan invers dari g(x) ?
Pembahasan :
- y=g(x)
- y=2x+1
- 2x=y-1
- x=(y-1)/2
- g-1(y) = (y-1)/2
- g-1(x) = (x-1)/2
Apabila fungsi g(x) inversnya ialah g-1(x) = (x-1)/2
3. Apabila ditemukan f(x) = 2x – 1, g(x) = x2 + 2. Selanjutnya tentukanlah :
- (g ◦ f)(x).
- (f ◦ g)(x).
- Apakah dapat berlaku sifat komutatif: g ◦ f = f ◦ g?
Jawab:
- (g ◦ f)(x) = g(f(x)) = g(2x – 1) = (2x – 1)2 + 2 = 4x2 – 4x + 1 + 2 = 4x2 – 4x + 3
- (f ◦ g)(x) = f(g(x)) = f(x2 + 2) = 2(x2 + 2) – 1 = 4x2 + 4 – 1 = 4x2 + 3
- Tidak berlaku sifat komutatif karena g ◦ f ¹ f ◦ g.
Nah itulah yang bisa quipper.co.id sampaikan mengenai materi fungsi komposisi, semoga ulasan kali ini bisa bermanfaat untuk kita semua.
Baca Juga :
